Проверка существования и единственности решения

Пусть профиль движется в несжимаемой вязкой среде с постоянной скоростью Uq под углом атаки а; v — кинематическая вязкость среды.

Выберем систему координат Oxyz, связанную с профилем. В рас­сматриваемом случае циркуляция потока на профиле изменяется, поэтому в силу теоремы о неизменности циркуляции по жидкому контуру, не пересекающему особенностей, с контура будут сходить и двигаться по потоку свободные вихри, циркуляция которых в данной математической модели останется постоянной. При этом свободные вихри будут параллельны присоединенным вихрям на профиле, т. е. оси Oz. Вязкость среды будем учитывать через скорость, индуциру­емую в ней вихрем единичной интенсивности, что позволит точнее учесть условие постоянства циркуляции в пространстве.

Так как задачу рассматриваем в линейной постановке при малых углах атаки, предположим, что свободные вихри движутся в плоскости Oxy со скоростью Uo.

Пусть профиль занимает отрезок [-1, 1] оси Ox. В силу того, что с задней кромки профиля сходит пелена свободных вихрей, скорости на ней должны быть конечными и, следовательно, к задней кромке ближайшей должна быть расчетная точка, а к передней — дискретный вихрь.

Дискретные вихри и расчетные точки расположим таким образом, чтобы дискретные вихри размещались в точках

xi = — 1 + (i — h, h = — , i = 1,n, (4.7)

V 4/ n

а расчетные точки были

хоі = хі + h = — 1 + (i — h, i = 1, n. (4.8)

Изменения всего вихревого слоя будем наблюдать через промежут­ки времени At = h/Uo. Для простоты положим Uo = 1. Координата свободного вихря, сошедшего с профиля в момент ts, в расчетный момент tr будет равна £sr = xn + (r — s + 1)At. Пусть циркуляция дискретного вихря в точке xi в расчетный момент времени tr равна Гіг, а циркуляции свободных вихрей, сошедших к этому времени с профиля, равны Ars, s = 1,…,r и постоянны во времени. Выполняя условие непротекания профиля в расчетных точках xoi, i = 1,…,n получим систему уравнений

где V* — нормальная составляющая скорости набегающего потока в расчетной точке xoj; шij — нормальная составляющая скорости в рас­четной точке xoj, индуцируемая вихрем единичной интенсивности, находящимся в точке xi; usjr — нормальная составляющая скорости в точке xoj, индуцируемая вихрем единичной интенсивности, находя­щимся в точке £sr в вязкой среде, причем из [26] следует, что

Дополним рассматриваемую систему уравнением, являющимся дис­кретным аналогом неизменности циркуляции во всем пространстве. Если профиль начал движение из состояния покоя, это уравнение будет иметь вид

Гіг + ^]ЛГ = 0, r = 1,2,3,…. (4.11)

i=1 s= 1

Таким образом, имеет место следующая система уравнений:

nr

Гіг Uij + ^>r Usjr = —V*, j = 1, n, r = 1,2,…, (4.12)

i=1 s = 1

nr

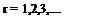£r* + 5>r = 0

i=1 s = 1

, tr) h ^ 6 (t ) ([2] — e-

(t-т )[3]/4vt

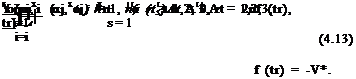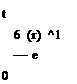
Полагая rjr = y (xjt, tr) h, Ars = 6 (ts)At, перепишем эту систему в виде

Матрица этой системы не вырождена и, следовательно, система разрешима [26]. С другой стороны, согласно результатам работы [28], предположим, что функции у (x, t) и 6 (t) принадлежат классу H* на соответствующих множествах, и получим, что предыдущая система аппроксимирует следующую систему интегральных уравнений:

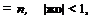
Воспользуемся формулами [26]:

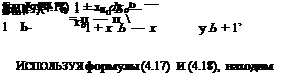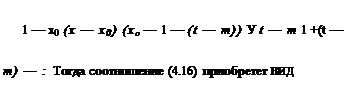где знак «-» для b > 1, а знак «+» для b < 1. Из последнего интеграла находим

Подставим выражение (4.2о) во второе уравнение системы (4.8). В результате это уравнение преобразуется к виду

Предположим, что 1 Є Ct [о, T] и f (о) = о. Тогда всякое непрерывное

при 0 <t ^ T решение уравнения (4.20) удовлетворяет интегральному уравнению

t

S (t) + k (t, r) S (r) dr = 2nf'(t), 0 <t < T,

0

1

/2 + t — t (t — t)3/4

+e-(t-T)2/4vt______ Vі — t (t + t)_______

2ut2 (/2 + t — t + Vt — t )

которое получено из (4.21) почленным дифференцированием по t. Легко видеть, что справедливо и обратное: всякое непрерывное при 0 < t ^ T решение уравнения (4.22) удовлетворяет также уравне­нию (4.21).

Умножим обе части уравнения (4.22) на Д и введем в рассмотре­ние новую неизвестную функцию y(t) = S(t)/t. Получим

0

В силу того, что имеют место следующие два неравенства:

2Vt k(t, x2) < M, 0 < x2 < t < T и 2nf’ (t)Vt < N, (4.24)

решение уравнения (4.23) существует и единственно. Его можно запи­сать в виде суммы такого ряда:

y (t) = У0 (t) — У1 (t) + У2 (t) — …, У0 (t) = 2nf (t)Vt,

тД

2ft k(t, r2) yk (r2) dr, k = 0,1,2,…. (4.25)

0

Поскольку уравнение (4.23) является следствием (4.21), решение исходного уравнения существует и имеет вид

Отсюда вытекает существование и единственность решения системы уравнений (4.20) и (4.21), т. е. справедлива следующая теорема.

Теорема Решение системы уравнений

t Є [0, T, f (0) = 0, f (t) Є Cl [0, T

существует и единственно.

Из этой теоремы следует правомочность рассмотренной выше моде­ли обтекания тонкого профиля.